Das Arithmeum in Bonn

Da braucht man am Rechnen gar nicht sehr interessiert zu sein, um zu schätzen, was gezeigt wird. Es ist dies vor allem die Entwicklung der Rechenkunst. Man braucht selbst nicht aktiv zu werden, außer man will es tun. Dann gibt es auch Möglichkeit diverse Hilfsmittel selbst auszuprobieren. Als zusätzliche Attraktion hat man im Museum die Wände mit ausschließlich geometrischen Malereien geschmückt - die Geometrie steht dabei in einem wunderbaren Kontrast und gleichzeitigen Ergänzung zur Arithmetik.

Die allerältesten Rechenhilfen, die wir kennen, stammen aus dem Zweistromland, näher bestimmt aus der Stadt Uruk, wo sie schon im vierten Jahrtausend vor Christus verwendet wurden. Sie werden Calculi genannt, nach kleinen Kieselsteinen. Die Rechensteine auf dem Bild links sind jedoch aus Ton, und damit leichter einzuritzen. Ihre Zahlenwerte sind unbekannt. Unser Wort "kalkulieren" kommt also über Latein (calculus = kleiner Stein) von diesen kleinen Steinen. Interessant ist auch, dass man in der modernen Medizin Gallen- oder Nierensteine als calculi bezeichnet.

Diese Tontafeln stammen ebenfalls aus Uruk, von etwa 3000 v. Chr. Sie zeigen Rechnungen, die die Zuteilung von Getreide (Gerste und Malz) als Basis für die Bierproduktion festhalten. Auf diesen Tontafeln wurden die Teilrechnungen normalerweise auf der Vorderseite angebracht, während das Endergebnis auf der Rückseite vermerkt wurde. Uruk war eines oder sogar "das" Zentrum, in dem die sumerische Kultur entstand und hatte um 3000 v. Chr. eine Blütezeit. Von dort stammen auch die ersten Schriftzeichen, die wir kennen.

Den Abakus gibt es in vielen Formen. Auch unser Kinderspielzeug, die sogenannten "Kugelschieber" mit den bunten Kugeln, die man auf kleinen Stangen verschieben kann, ist ein Abakus. Man kann vorzüglich darauf rechnen, auch multiplizieren und dividieren - aber das wissen nicht viele Europäer. Im Bild ist eine chinesische Variante aus dem 18. Jhd., ein Suanpan. Besonders in asiatischen Ländern wird der Abakus heute noch verwendet. Auch die ersten Formen des Abakus sind schon mehr als dreitausend Jahre alt.

Die Inka verwendeten einen Quipu als Rechenhilfe. Das waren Schnüre, die von einer waagrechten Schnur herabhingen und miteinander verknüpft werden konnten. Sie waren verschieden gefärbt, sodass man ihnen verschiedene Zahlenwerte zuordnen konnte. In Europa setzten sich - im 13. Jhd. von Frankreich ausgehend - sogenannte Rechenpfennige durch. Diese hatten jedoch keinen Eigenwert. Sie wurden auf ein Liniensystem gelegt und je nach Position symbolisierten sie verschiedene Werte. Das französiche Wort dafür ist "Jeton", eine Bezeichnung, die auch wir heute noch verwenden, zum Beispiel beim Pokern oder im Casino.

Der Schotte John Napier erfand Anfang des 17. Jahrhunderts zwar keine Maschine, aber immerhin Rechenstäbe, die das Multiplizieren erleichtern sollten. Jedes Stäbchen enthielt die Werte von zwei bis neun der ganz oben angeführten Grundzahl. Die Zehnereinheiten wurden durch einen Schrägstrich von den Einern getrennt. Dadurch kamen sie in dasselbe Feld wie die Einer der nächsthöheren Zahl des Multiplikanden. Sagen wir, dass wir 26 mal 6 rechnen wollen. Wir legen also die Stäbchen 2 und 6 nebeneinander und gehen auf die Reihe 6. Da finden wir 1/2 (6x2) beziehungsweise 3/6 (6x6).

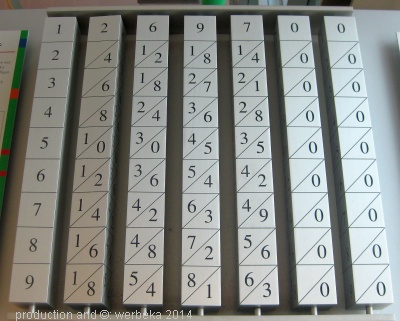Wenn diese Zahlen nebeneinander liegen sieht das so aus: 1/2 3/6. Nun addieren wir, was zwischen den Schrägstrichen steht (2+3) und kommen zum richtigen Resultat: 1, 2+3, 6 = 156 Noch ein Beispiel: 697 mal 4 gibt 2/4 3/6 2/8 = 2, 4+3, 6+2, 8 = 2788. Stimmt. Die Begrenzung der Stäbe ist, dass man beliebig hohe Zahlen multiplizieren kann, aber höchstens mal 9. Blaise Pascal erfand mit 19 Jahren, im Jahr 1642, eine Maschine, die addieren und subtrahieren konnte. Zwei Jahre später führte er eine verbesserte Version am Hof des französischen Sonnenkönigs, Ludwig XIV, vor.

Pascal bekam eine Art Patent vom König und baute zwanzig seiner Maschinen, verkaufte aber keine einzige. Im Bild links sehen Sie ein nachgebautes Modell der Pascaline. Bald entstanden anderswo ebenfalls mehr oder weniger verwendbare Rechenmaschinen verschiedenster Art.

Im Museum gibt es auch Lesetafeln mit Biografien hervorstehender Geister, wie eben Leibnitz, Napier oder Pascal. So erfährt man, dass Pascals Vater ein Steuerbeamter war und dass sein Sohn ihm bei den Berechnungen helfen musste. Not macht erfinderisch, daher brachte das den jungen Mann auf die Idee, eine Maschine zu bauen. Diese Rechentrommel von Jacob Leupold aus Leipzig, die er am Beginn des 18. Jhd. konstruierte, baut auf die Napierstäbe. Leupold hatte den Vorteil, dass er handwerklich und technisch geschult war und daher seine Maschine selbst herstellen konnte. Die meisten anderen waren ja davon abhängig, zum Beispiel einen Uhrmacher zu finden, dem sie ihre Erfindung aber erst detailliert erklären mussten, bevor er die Idee umsetzen konnte. Giovanni Poleni aus Venedig erfand um diese Zeit eine "rechnende Turmuhr", die mit Gewichtantrieb funktionierte. Seine Lösung mit den Sprossenrädern im Inneren, um die Werte in das Resultatwerk zu übertragen, war ein Vorbild für den Wiener Hofopticus und Mathematicus Anton Braun.

Das Sprossenrad dient zur automatischen Zehnerübertragung und wurde erst in den Maschinen des 19. und 20. Jahrhunderts allgemein gebraucht. Anton Braun entwickelte für Kaiser Karl VI eine Rechenmaschine. Als Poleni von dieser hörte, soll er aus Hochachtung seine eigene Maschine zerstört haben. Braun war nur für den Aufbau dieser Tischrechenmaschine verantwortlich. Das hübsche Gehäuse stammt von Johann Baptist Straub, einem Bildhauer aus München. Das Original der Maschine befindet sich heute im Kunsthistorischen Museum in Wien. Braun arbeitete an einer zweiten, verbesserten Version, als er 1728 plötzlich starb. Im Auftrag des Kaisers vollendete Philippe Vayringe aus Lothringen dieses Exemplar.

Der Pfarrer Philipp Matthäus Hahn entwickelte 1774 diese zylindrische Maschine für die vier Rechnungsarten bis zu elfstelligen Zahlen. Hahn betrieb neben seinem Hauptberuf als Kirchenmann auch eine feinmechanische Werkstatt. Seine Rechenmaschine steht im Original im Württembergischen Landesmuseum. Ein begabter Schüler Hahns, Jakob Auch, führte die Arbeit seines Lehrmeisters weiter und entwickelte im Jahr 1789 eine Addiermaschine mit einer neuen Zehnerübertragung über eine Schaltschiene.

Eine der letzten berühmten "handwerklichen" Maschinen ist die sogenannte "Arithmaurel", die 1849 durch die Zusammenarbeit der Uhrmacher Maurel und Jayet entstand. Es ist dies ein Beispiel dafür, dass Uhrmacher von sich selbst eine Rechenmaschine entwickelten. Während nämlich Uhren schon lange gefragt waren, wurden die Rechenmaschinen bisher oft als recht unnütze Gegenstände gesehen, die - außer von Wissenschaftern - kaum gebraucht wurden. Erst im 19. Jahrhundert veränderte sich dieser Trend. Der Nachteil der Arithmaurel war jedoch, dass sie viel zu filigran war. Sie zeigte wohl die Handwerkskunst dieser beiden Uhrmacher, aber sie war aus diesem Grund für den Dauergebrauch nicht geeignet.

In der zweiten Hälfte des 19. Jahrhunderts trat ein neues Zeitalter für die Rechenmaschinen ein. Zunächst begann die industrielle Erzeugung der Maschinen, was den Preis senkte und sie somit auch für kleinere Firmen erschwinglich machte. In Europa und in den USA entstanden jetzt viele verschiedene, seriell gefertigte Modelle. Der Schwede Odhner, der Deutsche Burkhardt und der Amerikaner Baldwin, sind Namen, die hierbei erwähnt werden sollten. Im Bild links eine Maschine von Burkhardt aus dem Jahr 1890.

Ein weiterer Fortschritt war die Zehnertastatur, also eine Maschine mit nur zehn Tasten insgesamt - statt zehn Tasten pro Stellenwert, wie sie teilweise noch bis Mitte des vorigen Jahrhunderts in Gebrauch waren. Im Bild links eine Maschine von 1934. Der Amerikaner Hubert Hopkins war ein Vorgänger dieses Systems, das schließlich die Welt eroberte. Allerdings musste der Stellenwert bei der Eingabe noch immer angegeben werden, wie bei der "Standard" im Bild unten links. Die nächste entscheidende Entwicklung war die von der manuell betriebenen Maschine zum Rechenautomaten. Eine der Voraussetzungen dafür war die Lochkarte. Der deutschstämmige Hermann Hollerith hatte die amerikanische Volkszählung 1890 mit einer solchen Maschine durchgeführt.

Das durchgreifend Neue daran ist, dass die Lochkarte auf binärer Basis funktioniert. Loch = 1, kein Loch = 0. Wenn man nun zum Beispiel wissen will, wie viele Männer (und Frauen) an einer Umfrage teilnehmen, dann markiert man "männlich" mit einem Loch, bevor man die Karte durch den Apparat schiebt. Nun wird bei jedem Mann ein Stromkreis geschlossen und eine Stufe weiter gezählt. Bei Frauen verhindert das Papier der Karte, dass der Stromkreis geschlossen wird. Auf diesem Binärsystem beruht ja auch der Computer, auf dem Sie gerade diese Zeilen lesen. Das Arithmeum zeigt auch die grundlegende Entwicklung der Computer und da nicht zuletzt der ständigen Verkleinerung der Schaltkreise, was in der zweiten Hälfte des 20. Jahrhunderts zu immer kleineren Geräten und immer größeren Speicherkapazitäten führte.

Der Computer und seine Entwicklung ist aber ein Thema für sich, das ich hier nicht behandeln will. Statt dessen möchte ich mit einem anderen Ehrfurcht einflößenden Bild schließen, das aus der ausgestellten Büchersammlung des Arithmeums stammt. Wenn Sie nach Bonn kommen, ist ein Besuch im Arithmeum auf jeden Fall zu empfehlen. Sie finden dort ein Gesamtkunstwerk, bestehend aus Museum, Ausstellung und Gebäude, das einen bleibenden Eindruck hinterlässt.

Zurück zu oder zum von