Arithmeum i Bonn

Men museet är verkligen fantastiskt. Man behöver inte alls vara intresserad av att räkna, för att uppskatta vad som visas. Det är framför allt räknekonstens utveckling. Man behöver själv inte bli aktiv, om man inte vill det. Men i så fall finns det möjligheter att på egen hand testa diverse hjälpmedel, som tagits fram genom tiderna. Som ytterligare attraktion har man tavlor på väggarna, som uteslutande består av geometriskt måleri. Geometrin bildar därigenom en fantastisk kontrast, men samtidigt en komplettering till aritmetiken.

De allra första hjälpmedel till räknandet, som vi känner till, härstammar från Mesopotamien, närmare bestämt från staden Uruk, där de användes redan under fjärde årtusendet före Kristus. De kallas Calculi, efter små stenar. Räknestenarna på bilden till vänster är dock av lera, så att man lättare kunde karva i dem. Fast deras talvärden känner vi inte till. Vårt ord "att kalkulera" kommer alltså över latinets (calculus = liten sten) från dessa små stenar. Intressant är också att man i den moderna medicinen betecknar gall- eller njurstenar som calculi.

Dessa lertavlor härstammar likaså från Uruk, från cirka 3000 före Kristus. De visar uppställningar över tilldelningen av spannmål (korn och malt) som tjänade som råmaterial vid öltillverkning. På dessa lertavlor markerades normalt delräkningarna på framsiden, medan det på baksidan fanns slutresultatet. Uruk var ett av, eller till och med "det" centrum, där den sumeriska kulturen växte fram. Kring 3000 före Kristus hade man en blomstringstid. Därifrån kommer även de första skrifttecknen, som vi känner till. Att kunna räkna och skriva bra är nog en grund för all civilisation.

En abakus finns det i många former. Även vår barnleksak med de färgade kulorna, som man kan skjuta fram och tillbaka på tunna stänger, är en abakus. Till den är den ryska versionen en förebild. Det går alldeles utmärkt att räkna på dessa (även multiplicera och dividera) - men det finns inte många europeer, som vet om detta. På bilden finns det en kinesisk variant från 1700-talet, en så kallad Suanpan. Speciellt i asiatiska länder används abakusen idag. Men även dess första former är mer än tretusen år gamla.

Inkaindianerna använde en Quipu som räknehjälp. Det var snören som hängde ner från ett vågrätt snöre och som kunde knytas med varandra. De hade olika färger, så att man kunde tillordna dem olika värden. Utgående från Frankrike kom i 1200-talets Europa så kallade räknepenningar i bruk. Dessa hade dock inget eget värde. De lades på ett system av linjer och allt efter position fick de olika värden. Det franska ordet för dem är "jeton", en beteckning, som vi använder ännu idag, till exempel i poker eller på kasino. Den stora utmaningen var däremot att kunna få till ett mekaniskt räknande.

John Napier från Skottland uppfann visserligen ingen räknemaskin i början av 1600-talet, men ändå räknestavar, som skulle förenkla multiplikationen. Varje stav markerades med ett värde från 2 till 9 gånger av det längst uppe angivna grundtalet. Tiotalen särades från entalen med ett snedstreck. Därigenom hamnade de i samma fält som entalen i multiplikandens näst högre tal. Säg, att man vill räkna 26 gånger 6. Vi lägger alltså stavarna 2 och 6 bredvid varandra och går ner till rad 6. Där finner vi 1/2 (6x2), respektive 3/6 (6x6).

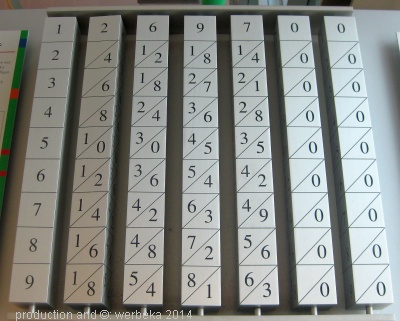När dessa tal ligger bredv id varandra ser det alltså ut så här: 1/2 3/6. Nu adderar vi det som står mellan snedstrecken (2+3) och får fram det rätta resultatet: 1, 2+3, 6 = 156 Ännu ett exempel: 697 gånger 4 ger 2/4 3/6 2/8 = 2, 4+3, 6+2, 8 = 2788. Det är korrekt. Stavarnas begränsning är dock att man visserligen kan multiplicera mycket höga tal, men högst gånger nio. När Blaise Pascal var nitton år, 1642, uppfann han en maskin, som kunde addera och subtrahera. Två år senare framförde han en förbättrad variant vid Ludvik XIV, den franske Solkungens, hov.

Pascal fick något slags patent av kungen och byggde tjugo stycken av denna maskin, men sålde inte en enda. På bilden till vänster ser man en rekonstruerad modell av denna Pascaline. Snart uppfanns det mer eller mindre användbara räknemaskiner av olika typ även på andra ställen.

På museet finns det också blad på vilka man kan läsa biografierna av dessa framstående genier, såsom just Leibnitz, Napier eller Pascal. Man får till exempel reda på att Pascals far var skattmas och att sonen var tvungen att hjälpa honom med beräkningarna. Nöden gör ju som bekannt uppfinningsrik - det var därför den unge mannen kom på idén att bygga sin maskin. Denna räknetrumma på bilden till vänster är av Jacob Leupold från Leipzig, som han konstruerade i början av 1700-talet. Den bygger på principen av Napierstavarna. Leupold hade en fördel. Han hade tillräckligt teknisk och hantverklig färdighet, så att han kunde bygga sin maskin själv. De flesta andra var ju beroende av att hitta till exempel en urmakare, som kunde tillverka deras uppfinning. Men då måste de först i detalj förklara hur den skulle fungera. Giovanni Poleni från Venedig uppfann vid denna tid en "räknande kyrktornsklocka", som drevs av vikter. Hans lösning med pinnhjulen i klockans inre, för att överföra värdena till resultatutlämningen, var en förebild för den wienske hovopticus och matematicus Anton Braun.

Pinnhjulet tjänar främst till att överföra tiotalen och kom inte till allmän användning förrän på 1800- och 1900-talen. Anton Braun utvecklade en räknemaskin för Kejsar Karl VI. När Poleni hörde talas om denna, ska han av högaktning för Braun ha förstört sitt eget verk. Braun var dock endast ansvarig för den inre uppbyggnaden av denna bordsräknemaskin. Det vackra höljet härstammar av Johann Baptist Straub, en bildhuggare från München. Maskinens original befinner sig idag i Konsthistoriska Museet i Wien. Braun arbetade på en andra, bättre modell, när han plötsligt dog år 1728. Med kejsarens uppdrag fullbordade Philippe Vayringe från Lorraine (fast då hette det Lothringen) detta exemplar.

Prosten Philipp Matthäus Hahn konstruerade 1774 denna cylinderformade maskin för de fyra grundräknesätten - och kunde därmed beräkna upp till elvasiffriga tal. Hahn drev vid sidan om sin huvudsysselsättning som präst även en finmekanisk verkstad. Hans räknemaskins original står i Landesmuseum i Württemberg. En begåvad elev till Hahn, Jakob Auch, fortsatte sin läromästares arbete och utvecklade 1789 en additionsmaskin med en helt annorlunda form av tiotalsöverföring.

En av de sista berömda "hantverkligt" framställda maskinerna är den så kallade "Arithmaurel", som uppkom genom samarbetet mellan två urmakare - Maurel och Jayet. Detta är ett av de fåtaliga exempel på att urmakare framställde en räknemaskin på eget bevåg. Medan klockor redan hade varit efterfrågade under några hundra år, ansågs räknemaskinerna hittills för det mesta som ganska onödiga prylar, som knappast behövde användas - annat än av vetenskapsmän. Först på 1800-talet förändrades denna trend. Arithmaurels nackdel var dock att dess uppbyggnad var alltför skör. Visserligen visade den de båda urmakarnas excellenta hantverksskicklighet, men den var inte lämpad för löpande vardagsbruk.

Under 1800-talets andra hälft uppstod en ny tidsålder för räknemaskinerna. Det började med att de från och med nu tillverkades industriellt, vilket sänkte priset avsevärt, så att de blev överkomliga även för små företag. I Europa och USA uppstod i rask följd många olika modeller, som tillverkades i långa serier. Svensken Odhner, tysken Burkhardt och amerikanen Baldwin är framstående namn, som inte ska glömmas bort i detta sammanhang. På bilden till vänster ses en maskin av Burkhardt från år 1890.

Ett annat framsteg var det numeriska tangentbordet, alltså en maskin med bara tio tangenter totalt - istället för tio per decimal enhet (som den på bilden till vänster från 1934). Sådana maskiner användes ända fram till mitten av förra århundradet. Amerikanen Hubert Hopkins var en föregångare till det nya systemet, som så småningom erövrade världen. Fast man var fortfarande tvungen att ställa in decimalvärdet för hand vid inmatningen, liksom på denna "Standard" på bilden nere till vänster. Nästa epokgörande utveckling var från en manuell driven maskin till räkneautomaten. En förutsättning för den senare var dock hålkortet. Hermann Hollerith, av tysk härstamning, genomförde den amerikanska folkräkningen 1890 med en sådan maskin.

Det genomgripande nya därvid var att hålkortet fungerar med en binär bas. Hål = 1, inget hål = 0. Om man nu till exempel vill veta hur många män (eller kvinnor) som deltar i en omröstning, markerar man "manligt" med ett hål, innan man kör kortet genom apparaten. Nu sluts det en strömkrets vid varje mans röst och det räknas ett steg vidare. Röstar en kvinna, förhindrar papperet att strömkretsen sluts. På samma kort kan man naturligtvis ha flera binära alternativ. På detta binärsystem beror ju också datorn, på vilken du just nu läser dessa rader. Arithmeum visar också datorernas grundläggande utveckling och då inte minst den enorma och stadiga förminskningen av de integrerade kretserna, vilket under andra hälften av 1900-talet ledde till allt mindre apparater och allt större minneskapaciteter.

Men datorn och dess utveckling är ett eget tema, som jag inte vill gå in på här. Istället skulle jag vilja avsluta med en bild som väcker enorm högaktning och som härstammar ur Arithmeums boksamling, där också somliga exemplar är utställda. Om du kommer till Bonn, så skulle jag rekommendera ett besök i Arithmeum å det varmaste. Du hittar där ett helhetskonstverk, som består av museum, utställningar, målningar och själva byggnaden. Detta kommer att lämna ett bestående intryck hos dig.

Tillbaka till eller till av